KURIKULUM MERDEKA BELAJAR

 

Kurikulum Merdeka Belajar Mulai Diterapkan pada 2022, Apa Itu Kurikulum Merdeka Belajar? Simak Penjelasannya

Aulia Rachma Dinantika

- 10 Juni 2022, 13:15 WIB

Kurikulum merdeka belajar/https://kurikulum.gtk.kemdikbud.go.id/ /

Dalam usaha untuk memulihkan kembali pembelajaran yang disebabkan oleh pandemi, Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi (Kemendikburistek) mengeluarkan kebijakan dalam pengembangan Kurikulum Merdeka.

Kurikulum ini diberikan kepada satuan pendidikan sebagai opsi tambahan dalam rangka melakukan pemulihan pembelajaran selama 2022-2024.

Kebijakan Kemendikburistek terkait kurikulum nasional selanjutnya akan dikaji ulang pada 2024 berdasarkan evaluasi selama masa pemulihan pembelajaran.

Kurikulum Merdeka adalah nama baru dari kurikulum prototipe yang resmi diluncurkan oleh Mendikbudristek Nadiem Anwar Makarim. Penasaran dengan bagaimana pengaturan dan penerapan Kurikulum Merdeka ini?

Pada saat ini, sekolah masih boleh memilih kurikulum yang akan digunakan di satuan pendidikan masing-masing. Pilihan kurikulum yang diberikan antara lain: Kurikulum 2013, Kurikulum Darurat, dan Kurikulum Merdeka.

Kurikulum Merdeka Belajar merupakan pengembangan dan penerapan dari kurikulum darurat yang diluncurkan untuk merespon dampak dari pandemi Covid-19.

Pengertian Merdeka Belajar adalah suatu pendekatan yang dilakukan supaya siswa dan mahasiswa bisa memilih pelajaran yang diminati.

Adanya pilihan bagi sekolah untuk menggunakan salah satu dari tiga kurikulum ini didasarkan pada dua alasan berikut ini:

1. Sekolah memiliki kewenangan dan tanggung jawab untuk mengembangkan kurikulum sesuai kebutuhan dan konteks masing-masing sekolah.

2. Kebijakan memilih kurikulum diharapkan dapat memperlancar proses perubahan kurikulum nasional karena dilakukan secara bertahap. Dapat dikatakan bahwa kebijakan memberikan opsi kurikulum sekolah merupakan salah satu upaya manajemen perubahan.

Esensi Kurikulum Merdeka adalah pendidikan berpatokan pada esensi belajar, di mana setiap siswa memiliki bakat dan minatnya masing-masing.

Tujuan merdeka belajar adalah untuk memitigasi ketertinggalan pembelajaran pada masa pandemi Covid-19 secara efektif.

Untuk saat ini Kurikulum 2013 tetap dapat digunakan sembari sekolah bersiap-siap untuk menerapkan kurikulum baru ini.

Setiap satuan pendidikan dapat menerapkan Kurikulum Merdeka secara bertahap berdasarkan kesiapan masing-masing.

Tidak dapat dipungkiri bahwa Indonesia telah mengalami krisis pembelajaran dalam waktu yang cukup lama.

Terdapat kesenjangan pendidikan yang mencolok antar wilayah dan kelompok sosial di Indonesia.

Dan hal ini diparah dengan adanya pandemi Covid-19 yang melanda kurang lebih 3 tahun ini.

Untuk memulihkan keadaan ini, diperlukan perubahan yang sistemik. Salah satunya melalui kurikulum sekolah.

Kemendikbudristek mengembangkan Kurikulum Merdeka dengan tujuan utamanya yaitu untuk memulihkan pembelajaran dari krisis yang sudah lama dialami anak-anak Indonesia.

Editor: Santi Yuliani

Sumber: Kemendikbud dan seputarlampung.com

Read More

BILANGAN BULAT NEGATIF

 Halo sahabat Pencinta Matematika, kali ini akan melanjutkan kembali pembahasan tentang Bilangan Bulat, yakni kita akan bahas Bilangan Bulat Negatif Beserta Contoh Soalnya. Yuk disimak..

Sebagaimana yang kita ketahui, bahwa bilangan bulat itu terdiri dari tiga jenis anggota bilangan bulat, yakni yang pertama adalah bilangan bulat positif, yang kedua bilangan bulat negatif, dan ketiga bilangan nol (0) yang mana bilangan ini tidak termasuk kedalam bilangan bulat positif maupun bilangan bulat negatif, tetapi bilangan nol (0) ini berdiri sendiri.

Sekarang mari Kita simak Pengertian Bilangan Bulat, Pengertian Bilangan Bulat Negatif dan Contoh Soalnya.

Pengertian Bilangan Bulat

Bilangan bulat adalah bilangan yang terdiri dari bilangan cacah (0, 1, 2, 3, …) atau ditulis (+1, +2, +3,+…) dan negatifnya yaitu (-1, -2, -3, …) -0 dalam bilangan bulat negatif adalah sama dengan 0 sehingga tidak lagi dimasukkan secara terpisah). Bilangan bulat itu tidak dapat ditulis dengan komponen desimal ataupun bilangan pecahan.

Sifat-Sifat Operasi Bilangan Bulat:

	Penambahan (+)	Perkalian (x)
Ketertutupan :	a + b   ialah bilangan bulat	a × b   ialah bilangan bulat
Asosiativitas :	a+(b+c) = (a+b)+c	a×(b×c) = (a×b)×c
Komutativitas :	a+b= b+a	a×b = b×a
Eksistensi Unsur-Unsur Identitas :	a + 0 = a	a × 1 = a
Eksistensi Unsur-unsur Invers :	a + (−a) = 0
Distribusivitas :	a×(b+c) = (a×b)+(a×c)
Tidak ada pembagi nol :		apabila a × b =0, jadi a = 0 atau b = 0 (atau kedua-duanyanya)

Setelah kita mengulas sedikit tentang pengertian bilangan bulat, maka selanjutnya kita langsung ke pembahasan pokok yaitu tentang pengertian Bilangan Bulat Negatif dan Contoh-Contoh Soalnya.

Pengertian Bilangan Bulat Negatif

Pengertian dari Bilangan Bulat Negatif ialah bilangan yang merupakan salah satu dari bilangan bulat yang memiliki tanda negatif (-) sebelum angkanya. Didalam bagan garis bilangan, bilangan bulat negatif ini yang berada di deretan sebelah kiri bilangan 0. Contoh bilangan bulat negatif yang sudah sering kita jumpai ialah sebagai berikut: -1, -2, -3, -4, -5, -6, … dan seterusnya.

Bilangan bulat negatif ini apabila semakin besar angka setelah tanda negatif (-) maka akan semakin kecil nilainya. Contohnya: -20 < -1 maka angka -20 lebih rendah atau lebih kecil nilainya dari pada angka -1.

Perhatikan Gambar Berikut :

Gambar Bagan Garis Bilangan Bulat Negatif

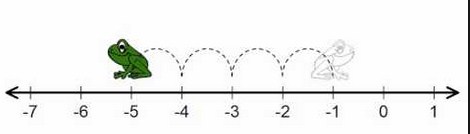
Perhatikan arah katak yang kekiri, semakin kekiri bilangan bulat negatif tersebut maka semakin kecil pula nilai suatu bilangan.

Bilangan Bulat Negatif Ganjil dan Bilangan Bulat Bulat Negatif  Genap

Sama hal nya dengan bilangan bulat positif, bilangan bulat negatif ini juga dibagi menjadi dua bilangan, yaitu bilangan bulat negatif ganjil dan bilangan bulat negatif genap.

• Bilangan Bulat Negatif Ganjil

Bilangan Bulat Negatif Ganjil ialah bilangan bulat negati yang tidak akan habis dibagi dua (2). Contoh : -1, -3, -5, -7, – dst..

• Bilangan Bulat Negatif Genap

Bilangan Bulat Negatif Genap ialah Bilangan bulat genap negatif yang habis dibagi dua (2) atau kebalikan dari bilangan bulat negatif ganjil. Contoh: -2, -4, -6, -8, – dst…

Contoh – Contoh Soal Bilangan Bulat

Mari kita sempurnakan pengetahuan kita dengan menyelesaikan beberapa contoh soal berikut :

Contoh Soal 1

1. Tentukan Hasil Pengoperasian Bilangan Bulat Positif dan Bilangan Bulat Negatif Dibawah Ini :

• 2+(-7) = 2–7 = -5
• 11+(-5) = 11-5 = 6
• (-7)+(-18) = -(7+18) = -25
• (-15)+7 = 7-15= -8
• (-25)+20= 20-25 =-5

Contoh Soal 2

2. Tentukan hasil hitung Campuran Bilangan Bulat Positif dengan Bilangan Bulat Negatif:

•     (-5)+15-5=  (-5)+10 = 10-5 =5
•      7-(-4)+10= 6+4+10 =21
•      (-55)-(-20)+40 = (-55)+20+40= (-55)+60=60-55=5
•     255+(-70)-(-120) = 255+(-70)+120=255-70+120=185+120  =305

Contoh Soal 3

3.  Hitunglah hasil dari  21:(3 – 10) + 4×(–2) = …
21 : (3–10)+4×(–2)
= 21:–7–8
= –3–8
= – 14.  Hitunglah hasil dari  25  + 7×(–5) adalah ….Jawab:25  +  7 × (–5)
= 25 – 35
= –105.  Hitunglah hasil dari –10 + 20×4 –(–6) :3 = …

Jawab:

–12+20×4–(–6):3
= –12 + 80 + 6 : 3
= 68+2
= 70

Contoh Soal 4

4.  Hitunglah hasil dari 15+(18:(–3))–((–2)×3)
adalah….

Jawab:
15+(18:(–3))–((–2) × 3)
= 15–6–(–6)
= 9+6
= 15

Contoh Soal 5

5.  Yang manakah Nlai n yang memenuhi (12+8)+(–3n)=–22 adalah…

Jawab:
(12+8)+(–3n)=–22
20–3n= –22
–3n=–22–20
–3n=–42
n=–3/–42= 14

Contoh Soal 6

6.  Hitunglah hasil dari 72–(510:8) = …

Jawab:
72– (510:8)= 72-63
= 9

Contoh Soal 7

7.  Mula-mula suhu suatu ruangan ialah 250° C. Kemudian ruangan tersebut akan dipergunakan untuk menyimpan telur ayam sebagai bibit, lalu suhunya diturunkan menjadi –30° C. Berapa besar perubahan suhu pada ruangan tersebut adalah ….

Jawab:
Perubahan suhu  = 25°C–(–3°C)
= 25°C+3°C
= 28°C

Dikutip dari rumusbilangan.com

Read More